time limit per test2 seconds

memory limit per test256 megabytes

inputstandard input

outputstandard output

Student Vladislav came to his programming exam completely unprepared as usual. He got a question about some strange algorithm on a graph — something that will definitely never be useful in real life. He asked a girl sitting next to him to lend him some cheat papers for this questions and found there the following definition:

The minimum spanning tree T of graph G is such a tree that it contains all the vertices of the original graph G, and the sum of the weights of its edges is the minimum possible among all such trees.

Vladislav drew a graph with n vertices and m edges containing no loops and multiple edges. He found one of its minimum spanning trees and then wrote for each edge its weight and whether it is included in the found tree or not. Unfortunately, the piece of paper where the graph was painted is gone and the teacher is getting very angry and demands to see the original graph. Help Vladislav come up with a graph so that the information about the minimum spanning tree remains correct.

Input

The first line of the input contains two integers n and m () — the number of vertices and the number of edges in the graph.

Each of the next m lines describes an edge of the graph and consists of two integers aj and bj (1 ≤ aj ≤ 109, bj = {0, 1}). The first of these numbers is the weight of the edge and the second number is equal to 1 if this edge was included in the minimum spanning tree found by Vladislav, or 0 if it was not.

It is guaranteed that exactly n - 1 number {bj} are equal to one and exactly m - n + 1 of them are equal to zero.

Output

If Vladislav has made a mistake and such graph doesn’t exist, print  - 1.

Otherwise print m lines. On the j-th line print a pair of vertices (uj, vj) (1 ≤ uj, vj ≤ n, uj ≠ vj), that should be connected by the j-th edge. The edges are numbered in the same order as in the input. The graph, determined by these edges, must be connected, contain no loops or multiple edges and its edges with bj = 1 must define the minimum spanning tree. In case there are multiple possible solutions, print any of them.

Examples

input

4 5

2 1

3 1

4 0

1 1

5 0

output

2 4

1 4

3 4

3 1

3 2

input

3 3

1 0

2 1

3 1

output

-1

【题目链接】:

【题解】

首先把那些在最小生成树中的边选出来;

并且从小到大排序;

然后从1一直到n;给每相邻的两个点之间按顺序分配这些n-条边即i-1到i的边权小于等于i到i+1的边权;

得到类似下面的生成树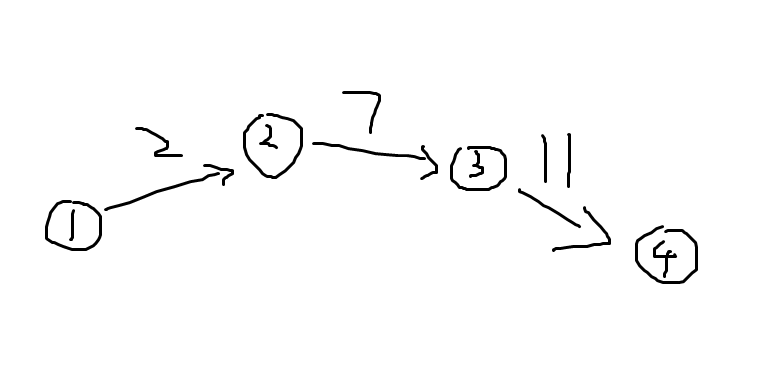

然后处理第n到第m条边(不在最小生成树中的自由边);

同样按照从小到大的顺序排序;

以插入两条自由边

8和12为例;

先插入8;

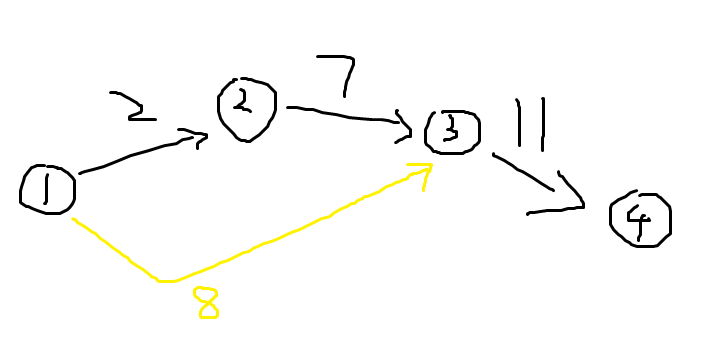为什么不插入在2上?因为不能有重边;

显然1..2这个节点已经是最小生成树了;接下来的问题就是要把3这个点和1和2这个生成树组合子啊一起;那问题就是要从1到3连一条边还是2到3连一条边;因为8>7显然这条边权为8的边不能加入到最后的最小生成树;所以可以添加这一条边而不影响最后的答案;

然后再插入12

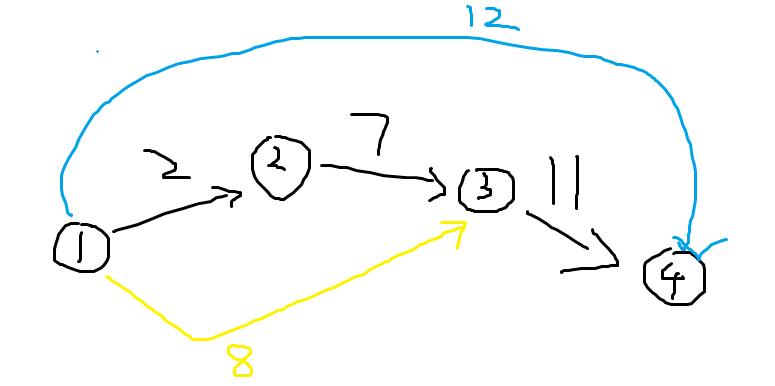这个过场相当于1-3号节点已经确定最小生成树的方案了；然后要加入一个节点4;那问题就变成要选3->4这条边还是选1->4这条边了;显然因为新插入的12>11所以在最终的最小生成树里面不会选12这条边;所以这样的加入方法是可行的;

再补充插入一个13

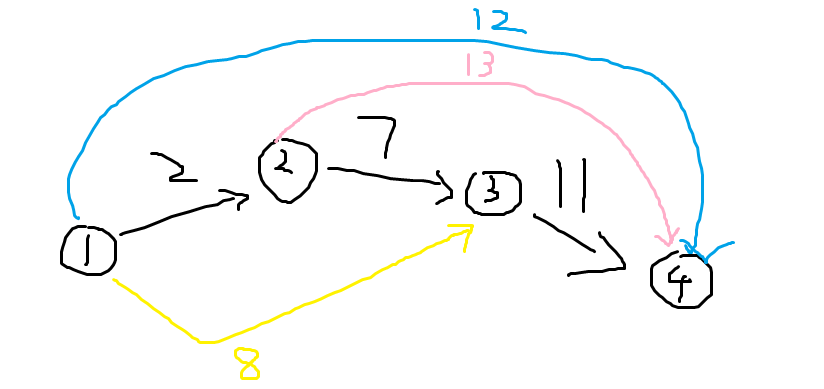还是同一个问题;

即1..3已经确定最小生成树的方式了；

要把那个4加入到最小生成树中；

则选择2->4还是3->4？

显然因为11<13所以会选择3->4这条边；而不会选择新插入的13那条边;

同时，我们不必要和1->4刚才那个插入的比较;因为那条边是比3->4大的;且在做MST的时候不会选那条边;所以不用比;

因为不能重边;

所以新加入的边的起点和终点的差都为1(对应到边上,边的差为2)；

然后我们按照优先终点不动先动起点的原则来构造这张图;

这样停留在终点越久;我们要加入的边大于终点-1到终点那条边的边权的机会更大;

因为是按照顺序搞的;所以如果遇到不满足大于等于前一条边的情况就要输出无解.

【完整代码】

#include 
     
      #include 
      
       #include 
       
        #include 
        
         #include